Wszystkich miłośników systemu Numicon i innych systemów multisensorycznych rozwijających kompetencje logiczne i matematyczne, chciałabym ucieszyć informacją, że już za rok ukaże się wyjątkowa książka pt. „Szkatułki – modelowanie kompetencji matematycznych dziecka z zespołem genetycznym” opracowywana przez zespół pod kierunkiem Arkadiusza Mańskiego z Uniwersytetu Gdańskiego. Udało nam się namówić Pana Arkadiusza, żeby uchylił rąbka tajemnicy wydawniczej i wprowadził nas w tematykę książki. Odkurzcie swoje klocki Numicon i inne obiekty wspomagające edukację symboliczną i matematyczną. Czas na przygodę z logiką i matematyką.
Artykuł autorski Szymona Mikołajewskiego, ucznia 3 klasy szkoły podstawowej nr 1 w Skarszewach i Pana Arkadiusza Mańskiego, nauczyciela akademickiego Uniwersytetu Gdańskiego. Tekst objęty prawami autorskimi. Kopiowanie treści, zdjęć i rysunków jest niedozwolone bez zgody Autorów.
Trochę wskazówek na dobry początek
Zrekonstruowanie procesów uczenia się arytmetyki przez dzieci z rozmaitymi zespołami genetycznymi jest ogromnym wyzwaniem. Jak do tej pory cały czas z nadzieją oczekujemy na jakiś dobry model, który być może pozwoli nawet na pewne przewidywania. Nie należy się jednak zniechęcać początkowymi niepowodzeniami, gdy jest na świecie kilku bardzo zdeterminowanych naukowców, którzy nad tym pracują (warto przeczytać: L.J. Rinaldi i in., (2019) Do the Colors of Educational Number Tools Improve Childrens Mathematics and Numerosity). Na samym początku jednak warto zastanowić się, jakie sensoryczne obiekty mogą ułatwić naukę liczb. A możliwości jest zaskakująco dużo: kostki, kasztany, patyczki, paski, kulki czy wreszcie kształty Numicon, obiekty ze zbioru Stern Arithmetic Block, a także osobliwe obiekty ze zbioru Numberjack.
Wybór więc może być dosyć trudny. Co zrobić? Nie ma jednej dobrej odpowiedzi, jednak dla młodszych dzieci, które przygotowujemy do edukacji szkolnej, warto w zabawach/grach zastosować różne obiekty i wybrać te, które najlepiej otwierają drzwi do celu np. do lepszego rozpoznawania liczb. Dla jednego dziecka bardziej przyjazny będzie zbiór klocków Numicon, a dla innego kolorowe kule, które w odpowiedni sposób można łączyć w większe całości. Nie należy też przekreślać roli tradycyjnych liczmanów np. kasztanów, korali itp. Oczywiście zanim nastąpi decyzja, każdy z rodziców powinien udać się na „łowy” aby znaleźć nauczyciela, który wyszuka to najbardziej optymalne narzędzie dla dziecka.
Sytuacja się komplikuje, gdy w zespole genetycznym diagności stwierdzą niepełnosprawność intelektualną. Posługiwanie się w projektowaniu edukacji włączającej dziecko w świat symboli matematycznych, nazewnictwem klinicznym (np. zespól Downa czy zespół Wiliamsa) sugerującym, że coś może być dobre dla dzieci z tym zespołem jest mocno ryzykowne. W naszym laboratorium (na Uniwersytecie Gdańskim) poszukujemy „bramek” prowadzących do umysłu dziecka. Gdy taką bramkę wraz ze ścieżką do niej prowadzącą namierzymy, wtedy możemy skonstruować narzędzia edukacyjne/naukowe, które wyniosą zdolności naszych Pociech na taki poziom, że będą postrzegać świat, jak nigdy wcześniej. Jest to właśnie najważniejszy postulat „Szkatułek”. Kiedy z Szymkiem zaczęliśmy poznawać dodawanie liczb, to kiedyś Mój a i niedawno Jego świat wzbogacił się o nowe „barwy” i „smaki”…
Szkatułka pierwsza – model I
Posłuchajcie tej opowieści o wodzie. Ona jest źródłem jednego z naszych matematycznych eksperymentów. Byłoby nam łatwiej pobiec nad morze w upalny letni poranek. Wziąć ciężką i lekką piłkę oraz materac. Zabawa w celowanie piłką w materac ukaże, że ciężar od samego początku odgrywa kluczową rolę w porównywaniu wielkości. Jeśli ta zabawa stanie się zaczynem pierwszej gry dydaktycznej, możemy dowiedzieć się, że receptory dzieci lubią nacisk i mogą stawić opór, a woda nie zawsze… Woda może ulec. I teraz wchodzimy do naszego laboratorium… Wraz z Szymkiem wlewamy wodę do szklanego naczynia. Mamy maleńką barkę o kształcie okrągłym, dobra będzie nakrętka od plastikowej butelki. Wtajemniczeni wiedzą, że trzeba wcześniej wziąć kilka obiektów i poeksperymentować aby wybrać ten, co dobrze pływa. Kiedy układamy „wybrańca” na powierzchni wody – pływa swobodnie. Obiekt zachowuje pewną stabilność. Pewnie Profesor Re’uven Feuerstein nie bałby się używać nawet takich abstrakcyjnych słów w interakcji z dziećmi z zespołem genetycznym, my też nie mamy z tym problemu. Nie potwierdzi tego wielu naukowców, ale są tacy, którzy są głęboko przekonani, że myślenie abstrakcyjne może być mocną stroną naszych dzieci.
Jeden z nas (Szymek lub Arek) dmuchając w barkę, burzy jej stabilność. Drugi (Arek lub Szymek) chwyta szklaną kulkę i unosi ją bardzo wysoko nad naczyniem z wodą. Ktoś trzeci daje sygnał i trzeba wtedy upuścić kulkę tak aby trafiła w pływającą barkę. Nie muszę Państwu mówić, że to jest gra. Wzajemny układ uników i celowych posunięć. Jeśli kulka upadnie na barkę, puszczający zyskuje 1 punkt (umówmy się na oznaczenie w systemie Numicon: pomarańczowy klocek, lub w systemie Stern Arithmetic Block: zielony, mały, pojedynczy sześcian). Jeśli kulka chybi, zanurzy się w wodzie i opadnie na dno, puszczający kulkę otrzymuje zero punktów (np. biały mały prostokąt).

Moment kiedy jeden z graczy trafi kulką w barkę uzyskując 1 punkt.

Zdarzenie gdy jednemu z graczy nie udaje się trafić w barkę i otrzymuje 0 punktów.
Ćwiczenie z wodą nie trwa długo. Na końcu każdy z graczy zgromadził sekwencję pomarańczowych, małych kwadratów i pewnie także białych. Białe kwadraty należy usunąć a połączyć pomarańczowe: najpierw w pasek, a następnie w kształt innego klocka Numiconu, którego wartość będzie sumą wszystkich zdobytych punktów – jedynek.

Stan po zakończeniu 5 rund. Widoczne są różne sekwencje efektów trafień i nie trafień w pływającą „barkę”.

Pierwszy krok w obróbce wyników. Redukcja zer.
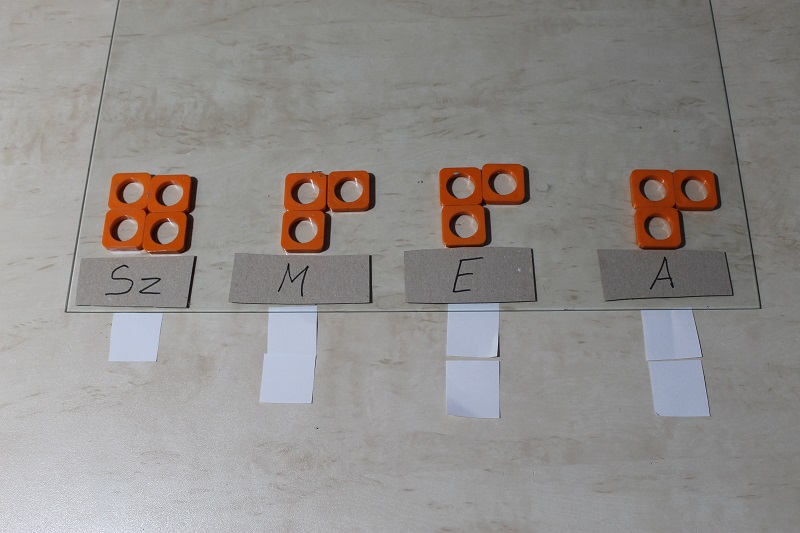
Drugi krok w obróbce wyników. Figuracja.
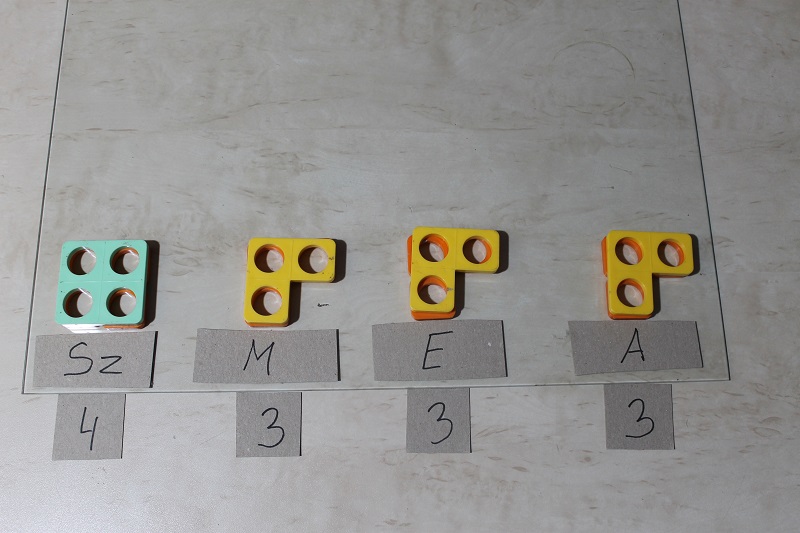
Trzeci krok w obróbce wyników. Zastosowanie algorytmu dodawania (dopasowanie).
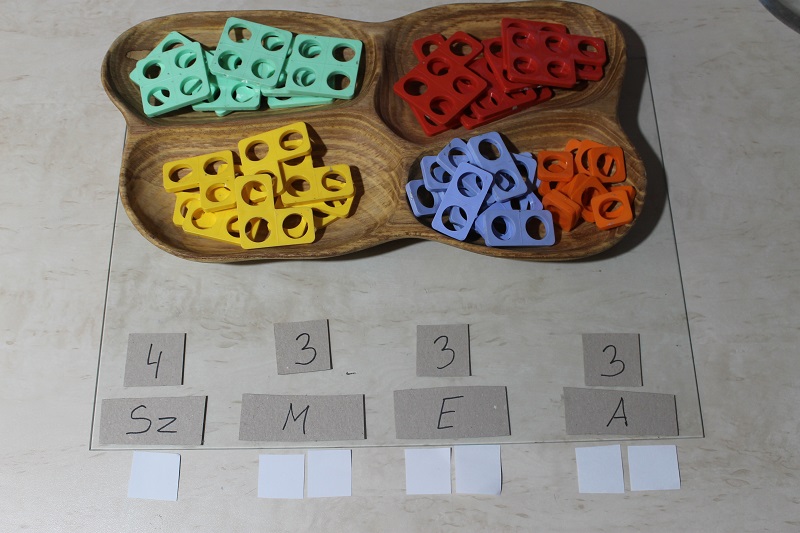
Ostatni krok. Prezentacja wyników po konwersji kształtu w symbol liczby.
Źródłem przedstawionej gry jest model, który w naszej „szkatułkowej” krainie nazwaliśmy „Modelem ciągłego poszukiwania równowagi”.
Ciąg dalszy - część druga!
Autorami tekstu są:

Szymon Mikołajewski, uczeń klasy III, Szkoła Podstawowa nr 1 w Skarszewach

Arkadiusz Mański, nauczyciel akademicki, Instytut Psychologii Uniwersytetu Gdańskiego
