Rozwijamy kompetencje logiczne i matematyczne naszych dzieci przy lekturze drugiej części cyklu o zastosowaniu systemu Numicon. Już za rok ukaże się wyjątkowa książka pt. „Szkatułki – modelowanie kompetencji matematycznych dziecka z zespołem genetycznym” opracowywana przez zespół pod kierunkiem Arkadiusza Mańskiego z Uniwersytetu Gdańskiego. Na łamach portalu Zakątek 21 Pan Arkadiusz wprowadza nas w tematykę książki. Odkurzcie swoje klocki Numicon i inne obiekty wspomagające edukację symboliczną i matematyczną. Czas na przygodę z logiką i matematyką.
Artykuł autorski Szymona Mikołajewskiego, ucznia 3 klasy szkoły podstawowej nr 1 w Skarszewach i Pana Arkadiusza Mańskiego, nauczyciela akademickiego Uniwersytetu Gdańskiego. Tekst objęty prawami autorskimi. Kopiowanie treści, zdjęć i rysunków jest niedozwolone bez zgody Autorów.
Szkatułka I – model II
W części pierwszej „Numicon – Szkatułki” opisaliśmy „Model ciągłego poszukiwania równowagi”, w którym Szymek albo Ja dmuchając w pływającą „barkę” decydujemy o losach gry (a właściwie o losie naszego partnera/ów w zawodach celowania kulką). Istnieje jednak coś takiego jak „ślepy” los. Nasz wpływ na poczynania tego władcy jest iluzoryczny tzn. prawie żaden. Jedni przyjmują jego rozkazy bez wzburzenia i oporu… Inni budują barykady myśląc, że pokonają ślepą siłę. I jedni i drudzy mają wewnątrz samych siebie dużo bezradności…
Nam potrzebny będzie sprytne wykorzystanie losu – działanie trochę sprzeczne ale dynamiczne… Dobrym przedmiotem edukacyjnym będzie tutaj np. moneta. Nikt nie zakwestionuje jej użycia na początku edukacji matematycznej. Jeśli dziecko lubi chipsy (co liczni uważają za głęboko niezdrowe) to szybciej wykryje pewną równowagę między zbiorem monet a kolorową torebką chipsów… Połączmy jednak monetę z systemem Numicon. Niech jedna ze stron pieniążka (np. orzełek) wskazuje na prawą stronę białej podkładki z zestawu Numicon, a druga (reszka) na lewą stronę białej podkładki. Ograniczmy zbiór klocków do tych, które oznaczają liczby od 1 do 5.
Mamy zatem 5 kolorów i możliwość znalezienia sposobu na losowanie barw. Jest tych sposobów niezwykle dużo. Można po prostu losować karty, po jednej ze zbioru kilku lub kilkunastu kart z kolorem po jednej stronie. Można rzucać kostką z kolorami na ścianach lub strzałką w specjalnie zaprojektowaną i powieszoną na ścianie tarczę z kolorami. Możliwości tworzenia i wymyślania sposobu jest sporo. W naszym szkatułkowym świecie ten model ma swoją nazwę – Model z wyborem losowym.
Teraz już można przystąpić do gry. Liczba graczy może być większa niż 2. Każdy w swojej kolejce losuje kolor i rzuca monetą. Otrzymuje w ten sposób informację o kształcie klocka (tym samym o liczbie!) i o stronie podkładki (planszy) na której ten klocek trzeba umieścić. Tablicę należy wypełnić w miarę możliwości. Gracz przegrany to ten, który nie może położyć (z różnych powodów) klocka na tablicy. Każdy ruch gracza zostaje też odnotowany, aby później można było porównać zdobyte punkty. Bardzo ciekawe są sposoby porównywania tych „zdobyczy” (patrz zdjęcie nr 9). Nie musimy budować wymyślnych struktur, które porównamy. Kiedy grają dwie osoby, wystarczy np. waga systemu Numicon. Oczywiście przy 3 i więcej graczach waga Numicon też może się przydać, ale to wymaga już większej liczby czynności i wytężonej uwagi.

Zdjęcie 8. Plan gry.
Kluczowe elementy: Z (zbiór klocków w drewnianym naczyniu uporządkowany kolorami), P (plansza do gry) i NOL (Narzędzia Operatu Losowania – kostka z kolorowymi ścianami i moneta).
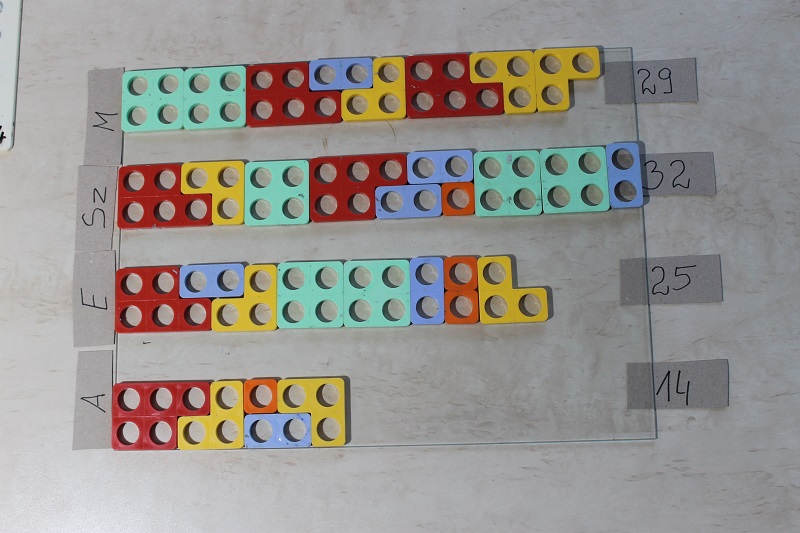
Zdjęcie 9. Sposób zobrazowania wyników.
Z pojedynczych klocków utworzono figury, które można porównywać ze względu na ich długość.
Szkatułka I – model III
W tym zakamarku szkatułki pierwszej kryje się prawdziwy, konstrukcyjny wulkan. Nie potrzeba specjalnych elementów, aby rozpocząć grę. Każdy nauczyciel–terapeuta ma w swoim warsztacie pracy jakąś odmianę torów kulkowych (czasem nazywa się je „kulodromami”). Uczniowie współczesnej szkoły rzadko na początkowych etapach edukacji budują takie konstrukcje, w których obserwować mogą obiekt przemieszczający się z punktu A do punktu B. Na trasie obiektu np. kulki wszystko jest dobrze zdefiniowane (przewidywalne) gdyż tor ogranicza ruch na boki, jednak na końcu (na „wylocie”) stan ten się zmienia.
Umieśćmy na końcu toru formę przypominającą dosyć szeroki murek. Przed nim układamy z klocków Numicon lub Stern Arithmetic Block pewna płaską lecz symetryczną mozaikę. W pewnej odległości od murku można ustawić tor, po którym może przemieszczać się kulka. Kulka wyrzucona z konstrukcji odbije się od muru i może zatrzymać się (zetknąć lub odbić) przy konkretnym klocku. Na początku nikt nie wie gdzie wyląduje kulka, lecz można zacząć przewidywać to miejsce – wskazywać klocek o określonej wartości liczbowej (nazwijmy model dla tych zadań: Model Przewiduję a Potem Sprawdzam). Możemy budować mozaiki z klocków Numicon różnej wartości. Warto najpierw użyć klocków z dwóch zbiorów wartości (1 i 2), potem trzech (1, 4 i 5), a potem czterech i na końcu pięciu.
Wielu laików (tzn. ludzi, którzy nie znają bliżej naszych dzieci) spojrzy z niedowierzaniem na tę grę, gdyż spotkać można w przekonaniach tzw. opinii publicznej pogląd o braku zdolności przewidywania u naszych dzieci. Wtajemniczeni wiedzą już dobrze, że te poglądy lekko trącą „myszką”. W tej grze trzeba w jakiś sposób zapisywać wyniki (pozostawiać ślad przewidywania). Co ważne – nagradzamy dodatkowym punktem trafne przewidywanie. Jeśli przed rozpoczęciem zjazdu kulki powiem (postawię hipotezę), że kulka zatrzyma się przy kształcie czerwonym (5 w Numiconie) i tak się stanie, otrzymuję dodatkowo jeden punkt do tych, które wskaże kulka. Zdjęcie poniżej (zdjęcie nr 10) to przybliża. Ostatecznie każdy z graczy buduje drogę z klocków Numicon o szerokości 2. Wygrywa ten, którego droga będzie dłuższa. Możemy też zważyć na wadze systemu Numicon klocki graczy w celu wyłonienia zwycięzcy.

Zdjęcie 10. Przestrzenne rozmieszczenie elementów do gry.
Widzimy: wyrzutnię, murek i symetryczną mozaikę z klocków Numicon.
Podsumowując…
Zajrzeliśmy do trzech zakamarków pierwszej Szkatułki, a zakamarków w tej szkatułce jest dosyć dużo. Wśród licznych opisów gier i zadań, znajdują się w Niej takie modele, które mają charakter wzorców do tworzenia nowych zadań i kontekstów edukacyjnych. Każdy model zawiera również pewną myśl/ideę/koncepcję – fragment rusztowania jaki możemy w naszych dzieciach zbudować.
Przykładowo:
- Model ciągłego poszukiwania równowagi. Jego opis jest dosyć obszerny lecz w książce „Szkatułki” zostanie (tak jak wszystkie) szczegółowo przedstawiony. Kiedy konstruujemy zadania na bazie Modelu ciągłego poszukiwania równowagi, milcząco zakładamy, że całe dziecko może być aktywne (aktywność zakłada powroty do punktu równowagi np. aby ponownie się od niego oddalić). Przestrzeń staje się miejscem „akcji” i każdy jej element zostaje włączony do pracy. Pomieszczenie, w którym działamy staje się swoistym laboratorium. Nic nie jest w tym laboratorium z góry zdefiniowane.
- Model z wyborem losowym. Tu zakładamy, że niepewność jest też udziałem dziecka, a w oczekiwaniu na wynik mogą powstać pewne własne pragnienia związane z wartością tego wyniku. Na tym etapie nie trzeba ich wyrażać środkami zaawansowanymi.
- Model przewiduję a potem sprawdzam. Ten model powiązany jest z Modelem z wyborem losowym. W zadaniach opartych na tym modelu trzeba jednak wyrazić swoje przewidywanie wyniku. To zostaje zanotowane i po wykonaniu działania następuje porównanie. Możemy nagrodzić zgodność obu wyników dodatkową premią lub oznaczyć różnicę między wynikami. Drugi sposób jest trudniejszy i nie udało się nam na razie uczynić go bardziej dostępnym poznawczo dziecku z zespołem genetycznym na wczesnych etapach edukacji symbolicznej.
Ciąg dalszy nastąpi... A dla Czytelników, którzy ją przez przypadek ominęli - część pierwsza!
Autorami tekstu są:

Szymon Mikołajewski, uczeń klasy III, Szkoła Podstawowa nr 1 w Skarszewach

Arkadiusz Mański, nauczyciel akademicki, Instytut Psychologii Uniwersytetu Gdańskiego
